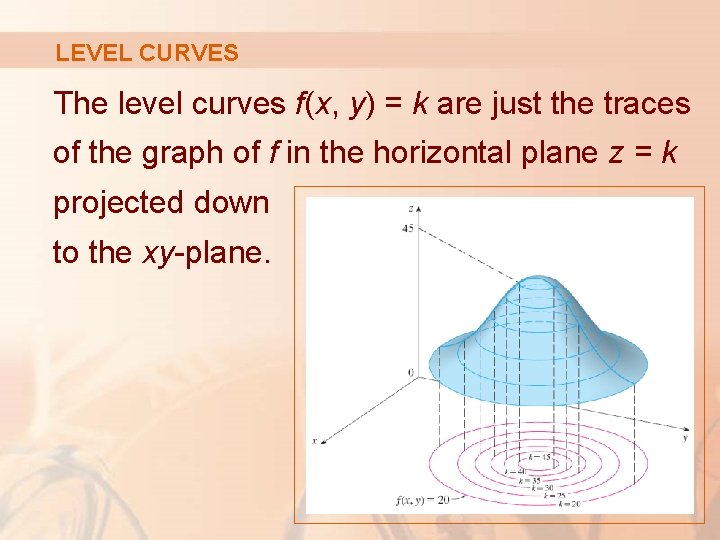
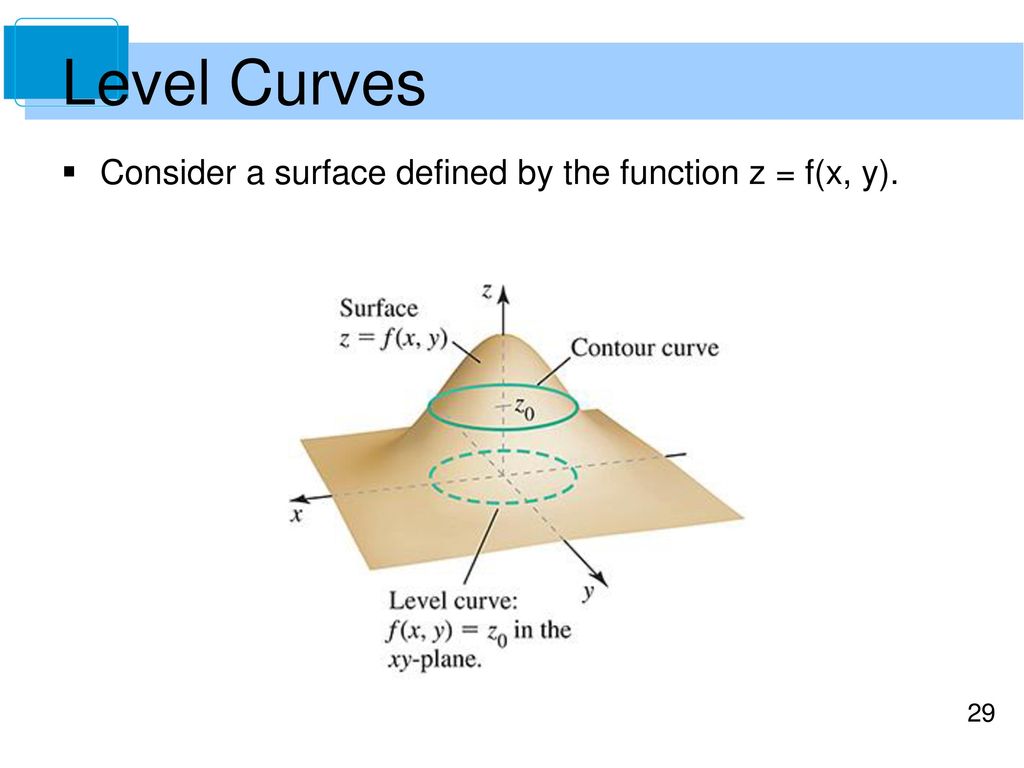
1 27 27 2k ?Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below isLevel curves are always graphed in the x yplane, x yplane, but as their name implies, vertical traces are graphed in the x z x z or y zplanes y zplanes Definition Consider a function z = f ( x , y ) z = f ( x , y ) with domain D ⊆ ℝ 2

Level Curves In The Plane E 0 Log A 0 When The Error E M On The Download Scientific Diagram
Level curves example
Level curves example-The level curves of $f(x,y)$ are curves in the $xy$plane along which $f$ has a constant valueThe curve $100=2x2y$ can be thought of as a level curve of the function $2x2y$;



How To Sketch Level Curves Youtube
Level Curves Recall that a level curve is a curve that passes through some perpendicular "level" of a surface When we have a surface {eq}z = f (x,y) {/eq}, level curves are of the form {eq}z = kIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the functionThe set of all points (, ) in the plane such that is called a level curve of (with value ) Contributed by Osman Tuna Gökgöz (March 11) Open content licensed under CC BYNCSA
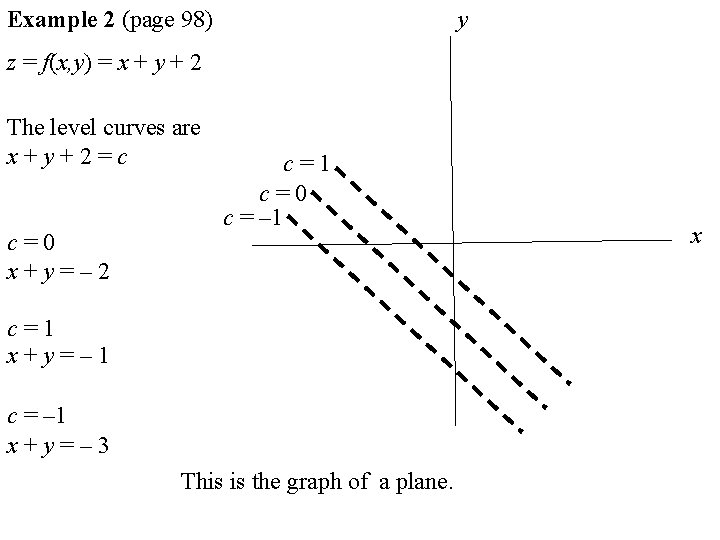
Chapter 1 Curves 11Course description Instructor Weiyi Zhang Email weiyizhang@warwickacuk Lecture time/room Tuesday 10am 11am MS04 Thursday 12pm1pm L5131 Surfaces and Level Curves (page 475) CHAPTER 13 PARTIAL DERIVATIVES 131 Surfaces and Level Curves The graph of z = f (x, y) is a surface in xyz spaceWhen f is a linear function, the surface is flat a plane) When f = x2 y2 the surface is curved (a parabola is revolved to make a bowl)When f = x2 y2 the surface is pointed (a cone resting on the origin)The tangent plane(or the graph), the tangent line of the level curve, the normal line of the level curve Tangent plane and the normal line of the graph are in xyz space while the things related to level curve are in xy plane Tangent plane and normal line of graph Tangent plane is
119 The normal line to a curve at a point ppp is the straight line passing through ppp perpendicular to the tangent line at pppFindthetangentandnormallinesto the curve γγγ (t)=(2cost − cos2t,2sint − sin2t)atthepointcorrespondingto t = π/4 1110 Find parametrizations of the following level curves (i) y2 = x2(x2 − 1)And we slice that function with a plane along specific values of one of the variables (typically the zdirection), and then project that intersection onto the twodimensional plane We repeat this process over and over at different levels of z to to obtain a series of embedded curves that trace out the shape of the graph at fixed heightsDraw the level curves (in the x y plane) for the given finction f and specified values of c Sketch the graph of z=f(x, y) f(x, y)=\left(100x^{2}y^{2}\right



Energy Level Curves Of The Hamiltonian Given By Equation 11 On The Download Scientific Diagram



Setting The Sketch Plane Of Model Lines Created By Curves Fromcadlayers Bimorph Node Developers Dynamo
So level curves, level curves for the function z equals x squared plus y squared, these are just circles in the xyplane And if we're being careful and if we take the convention that our level curves are evenly spaced in the zplane, then these are going to get closer and closer together, and we'll see in a minute where that's coming fromJan 14, · The family of planes a x b y c z = d define, implicitly, a family of functions z = f (x, y) = 1 c d − a x − b y, for c ≠ 0 To find the level curves of this function, you fix z = k for an arbitrary constant kOliver Knill, Harvard Summer School, 10 Chapter 2 Surfaces and Curves Section 21 Functions, level surfaces, quadrics A function of two variables f(x,y) is usually defined for all points (x,y) in the plane
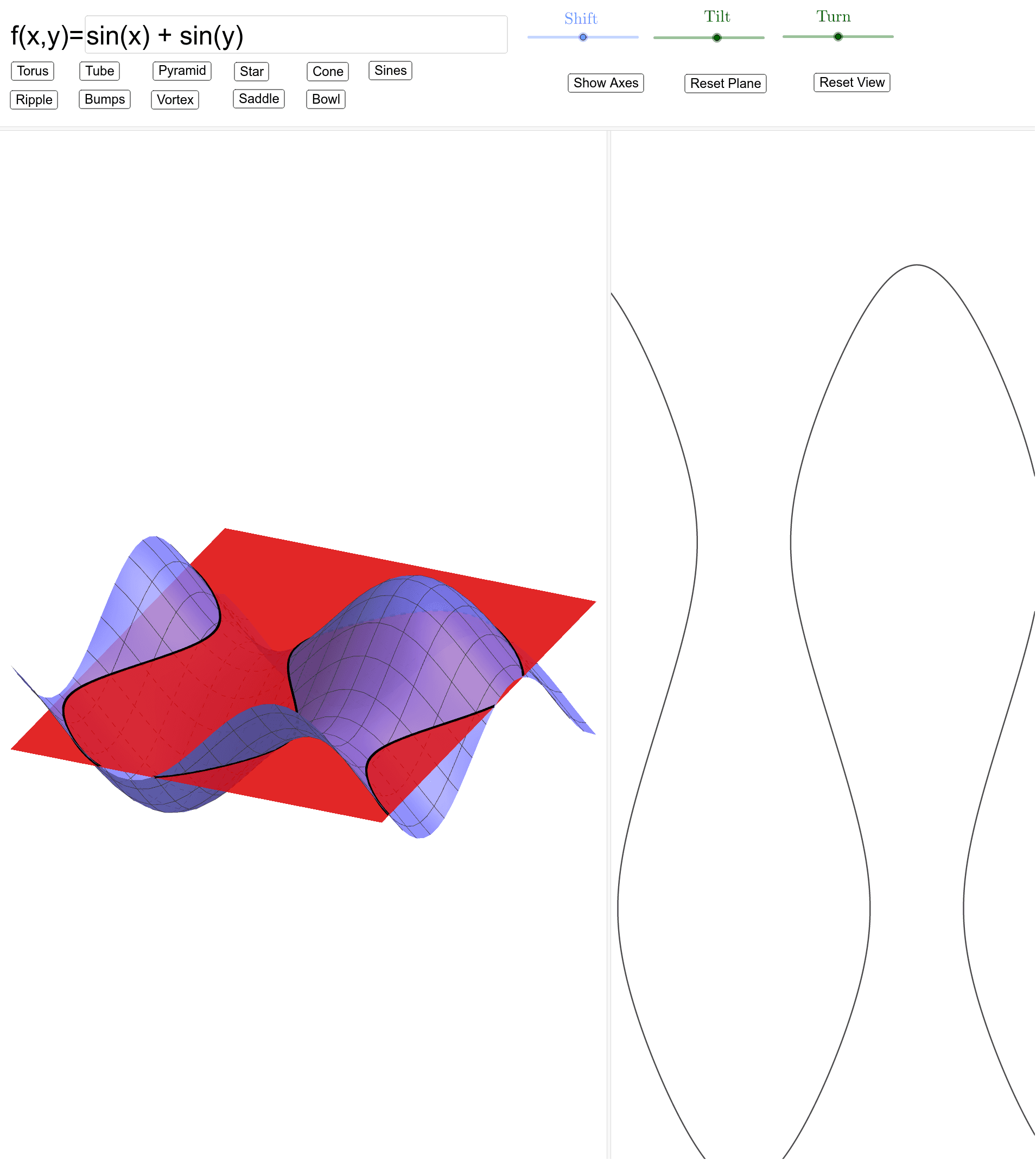


Level Curves From 3d Surfaces Geogebra
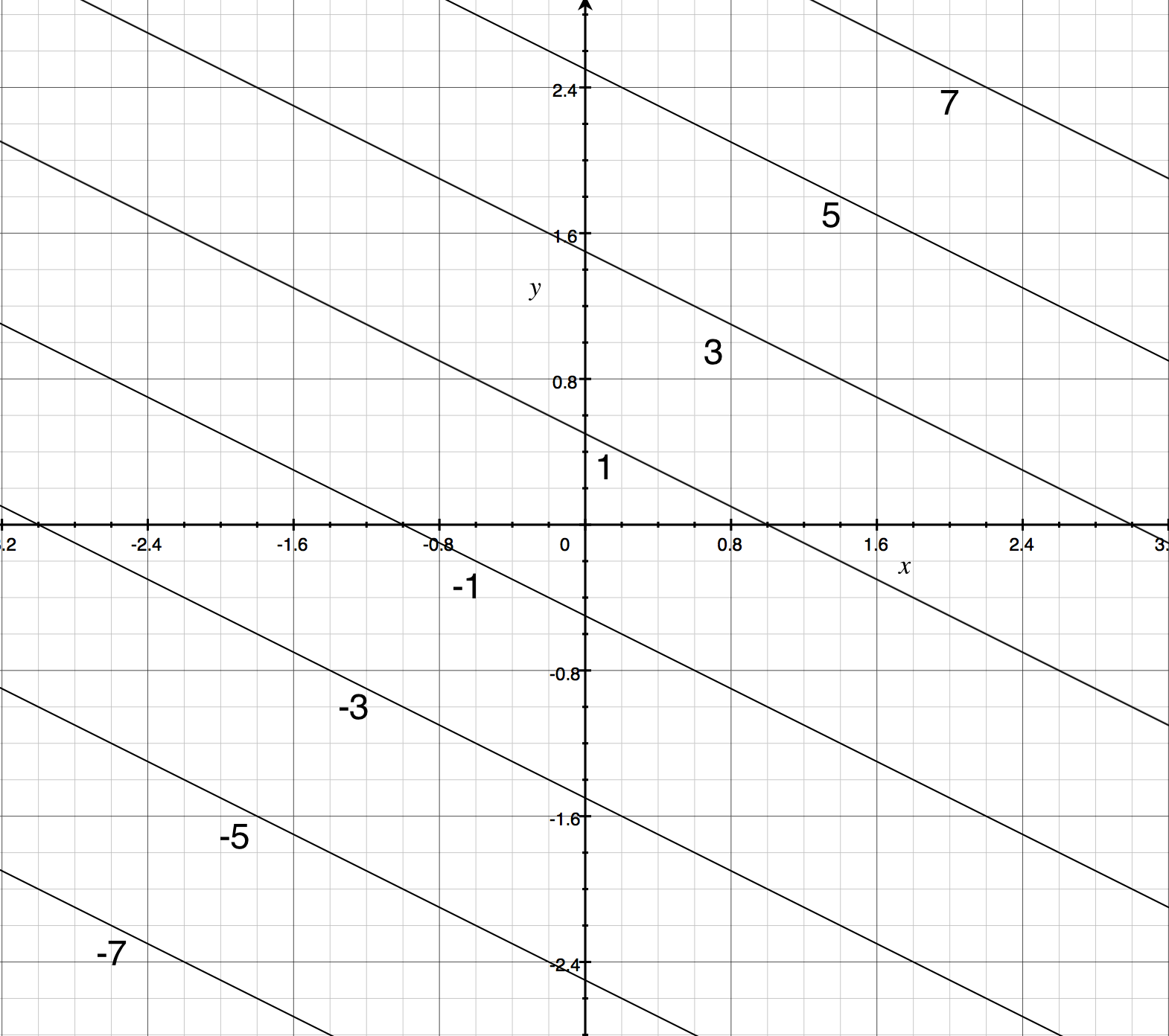


Contour Maps Article Khan Academy
Prove that the level curves of the plane a xb yc z=d are parallel lines in the x y plane, provided a^{2}b^{2} \neq 0 and c \neq 0Relief Functions and Level Curves Purpose The solution of the equation f(x, y) = C can be visualized graphically by plotting the function together with the plane z = C The curve generated by this intersection is often referred to as a level curve Note that this curve lies on the surfaceLevel Curves Added May 5, 15 by RicardoHdez in Mathematics The level curves of f(x,y) are curves in the xyplane along which f has a constant value Send feedbackVisit WolframAlpha SHARE Email;



Gate Ese Level Curves And Surface Of A Function In Hindi Offered By Unacademy


Sketching Surfaces In 3d
Fig 1 shows three level curves with tangent and curvature vectors marked Let P be a point in the xyplane as indicated and consider the level curve passing through that point Let ~r(s) be a parameterization by arc length of this level curve, with ~r(0) = P The derivative ~r0(0) is the tangent vector to the level curve at point PApr 12, 18 · The graph of this plane curve appears in the following graph Figure \(\PageIndex{5}\) Graph of the plane curve described by the parametric equations in part c This is the graph of a circle with radius \(4\) centered at the origin, with a counterclockwise orientation The starting point and ending points of the curve both have coordinatesLevel curves for a function $z=f (x,\,y) \, D \subseteq {\mathbb R}^2 \to {\mathbb R}$ the level curve of value $c$ is the curve $C$ in $D \subseteq {\mathbb R}^2



Solutions To Homework 1 1 The Level Curves Are Determined



Level Curves
Surfaces and Contour Plots Part 6 Contour Lines A contour line (also known as a level curve) for a given surface is the curve of intersection of the surface with a horizontal plane, z = cA representative collection of contour lines, projected onto the xyplane, is a contour map or contour plot of the surface In particular, if the surface is the graph of a function of two variables, say zBy combining the level curves f (x, y) = c for equally spaced values of c into one figure, say c = − 1, 0, 1, 2, , in the x y plane, we obtain a contour map of the graph of z = f (x, y) Thus the graph of z = f (x, y) can be visualized in two ways, one as a surface in 3 space, the graph of z = f (x, y),1624 // Summary for how to sketch level curves Whenever you're dealing with a multivariable function, the graph of that function will be a threedimensional figure in space If you take a perfectly horizontal sheet or plane that's parallel to the xyplane, and you use that to slice through your



Level Curves Calculus



Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download
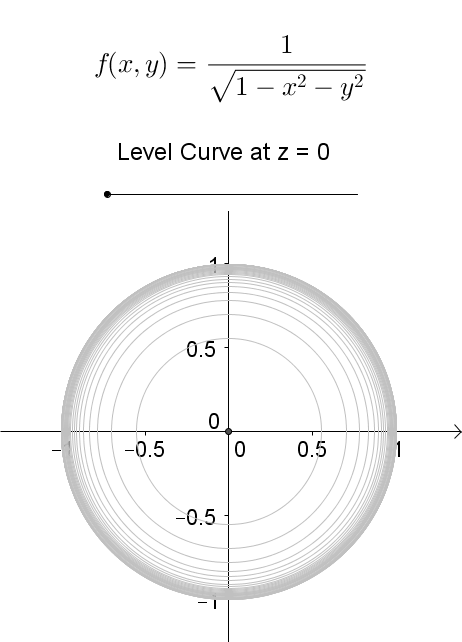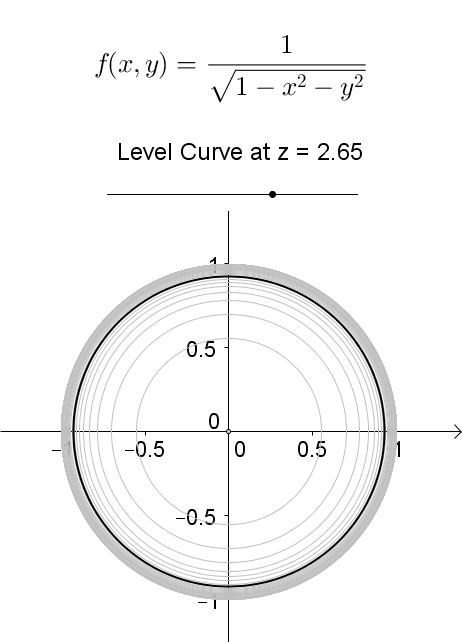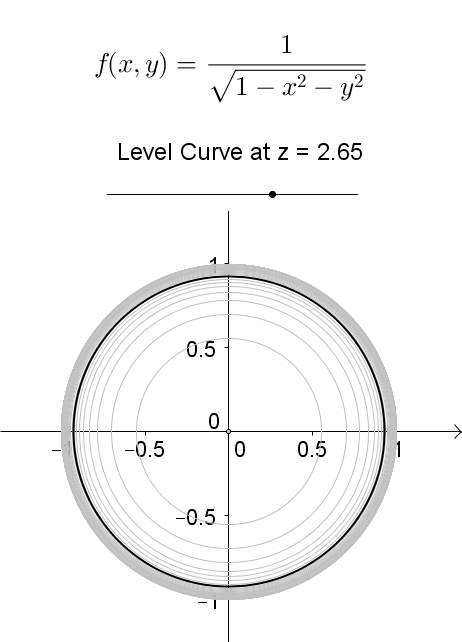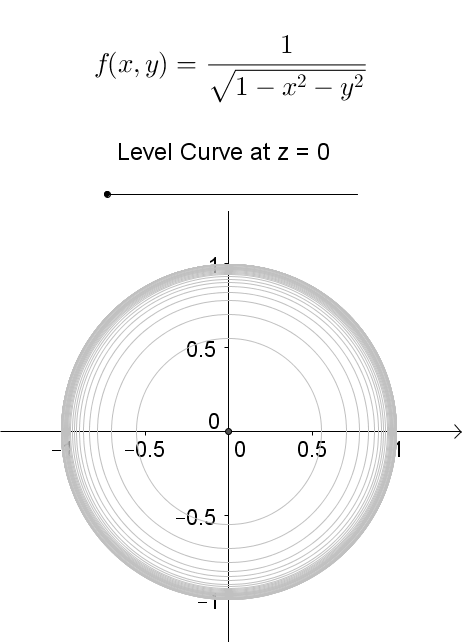
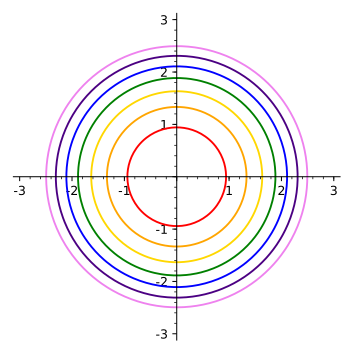
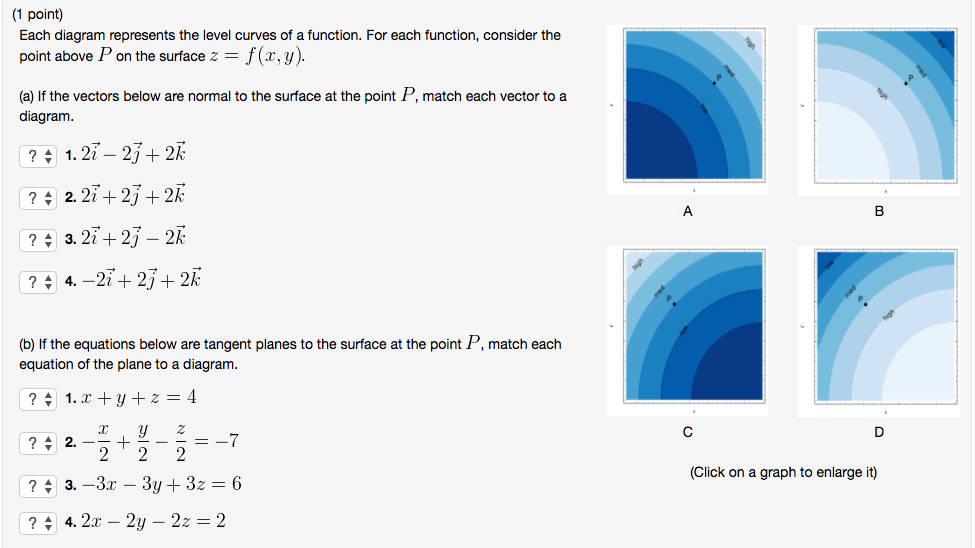
Nov 17, · Definition level curves Given a function f(x, y) and a number c in the range of f, a level curve of a function of two variables for the value c is defined to be the set of points satisfying the equation f(x, y) = c Returning to the function g(x, y) = √9 − x2 − y2, we can determine the level curves of this function(1 point) Each diagram represents the level curves of a function For each function, consider the point above P on the surface z = f(x, y) (a) If the vectors below are normal to the surface at the point P, match each vector to a diagram ?The level curves (or contour lines) of a surface are paths along which the values of z = f (x,y) are constant;


14 Partial Derivatives Partial Derivatives So Far We



Calculus Iii Exam Iii Notes And Links Math Resources Vosbury V2 0
Sep 19, 17 · 1330 // What are the level curves for a plane?0, so the curve's tangent lines all lie in the plane through P 0 normal to rf We call this plane the tangent plane of the surface at P 0 The line through P 0 perpendicular to the plane is the surface's normal line at P 0 P Sam Johnson (NIT Karnataka) Normals to Level Curves and Tangents September 1, 19 4 / 30Level curves (f(x,y) = k) constraint curve To maximize f subject to g(x,y) = 0 means to find the level curve of f with greatest kvalue that intersects the constraint curve It will be the place where the two curves are tangent Two curves have a common


Level Curves And Contour Plots Mathonline



C Level Curves Are Straight Lines Y X C Parallel To The Line 14 1 Function N D No Boundary Points N E Both Open And Closed N 1 Unbounded N A Domain Set Of All
The level curve de ned by f(x;y) = 0 is And the level curve de ned by f(x;y) = 4 is Notice that the crosssections lie in the space of R3, while the level curves in R2 This is because we think of level curves as subsets of the domain corresponding to a function value The crosssections refers to the intersection of the graph of the functionV 2 21 2j 2K A B ?Then the curves obtained by the intersections of the planes, with the graph of are called the Level Curves of From the definition of a level curve above, we see that a level curve is simply a curve of intersection between any plane parallel to the axis and the surface generated by the function



The Boundary D Of The Region D In The V 1 V 2 Plane Is Given By The Download Scientific Diagram
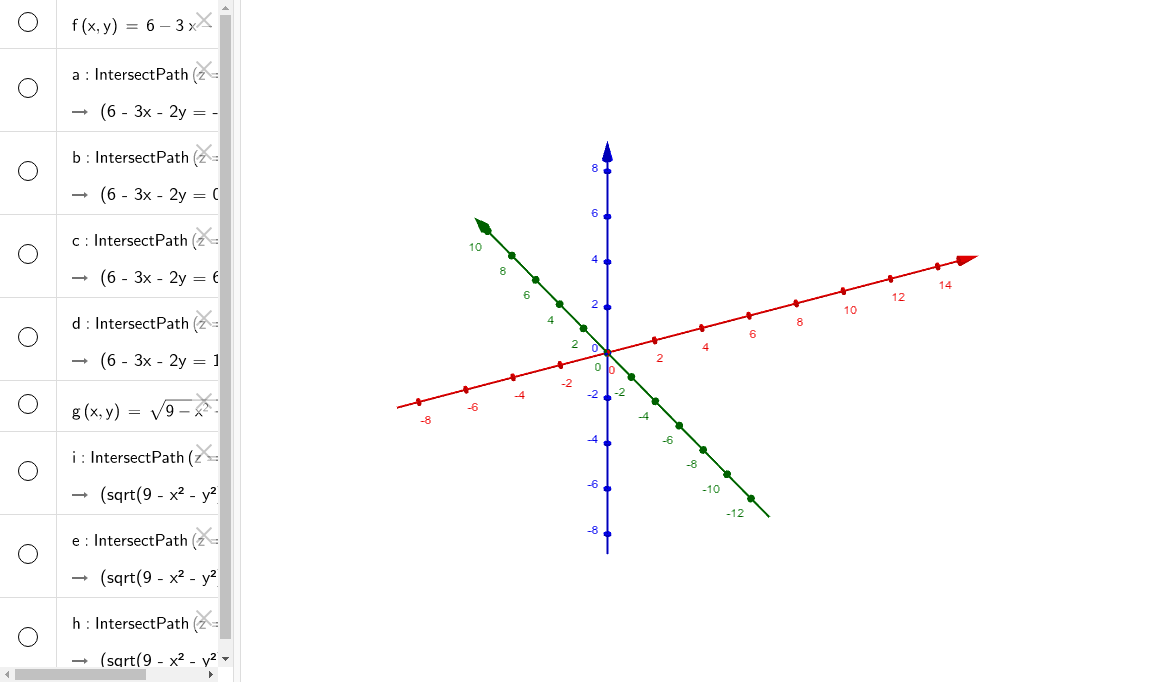


Level Curves Of Plane And Sphere Geogebra
The complete stability map in the parameters plane is the set of level curves f(x,y) = z where f is a "stability indicator", eg a function giving the (real part of the) rightmost eigenvalue governing the system dynamics, in which case z = 0 Hence typically f corresponds to an exact (orA level curve of a function f (x, y) is the curve of points (x, y) where f (x, y) is some constant value A level curve is simply a cross section of the graph of z = f (x, y) taken at a constant value, say z = c A function has many level curves, as one obtains a different level curve for each value of c in the range of f (x, y)Level Curves and Plane Sections The Cross Section tutor is used to investigate the level curves and plane sections of a surface Alternative Content Note In Maple 18, contextsensitive menus were incorporated into the new Maple Context Panel, located on the right side of the Maple window If you are using Maple 18, instead of right



Level Set Examples Math Insight
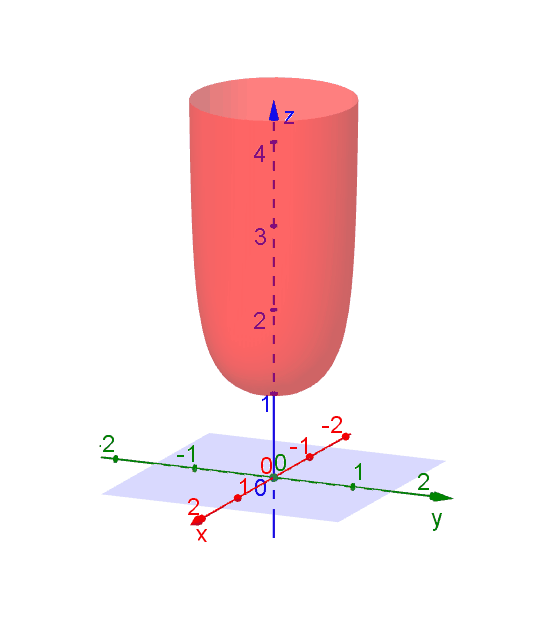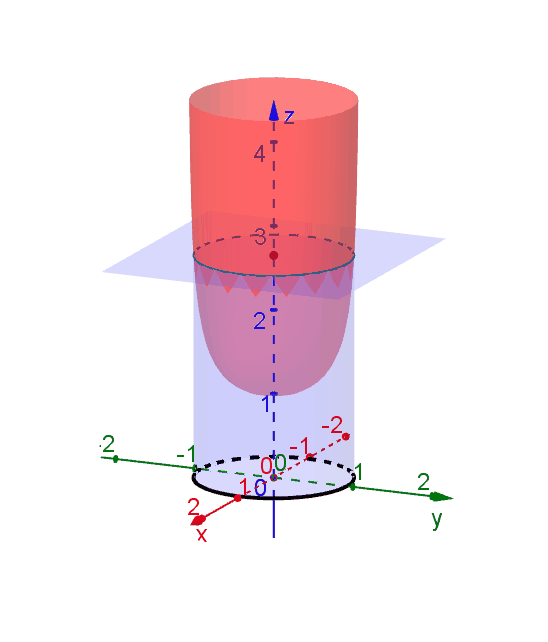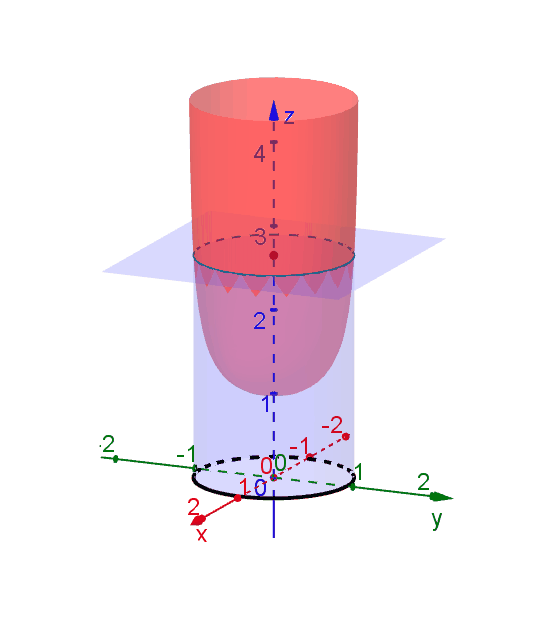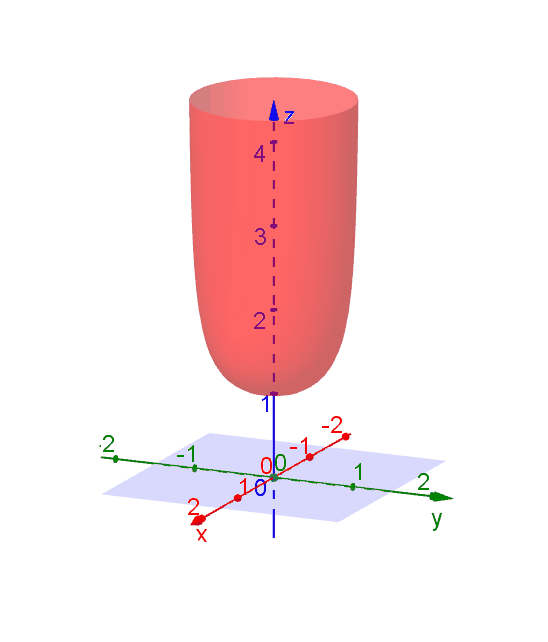


Level Curves Geogebra Dynamic Worksheet
Level Curves One of the most useful and common methods for visualizing functions (or surfaces) of two varibles is a Contour Map in which points of constant elevation are joined in a 2D plane to form level curves (or contour curves)LEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;May 26, · The level curves of the function z = f (x,y) z = f (x, y) are two dimensional curves we get by setting z = k z = k, where k k is any number So the equations of the level curves are f



Math 27 Winter 12 Assignment 2 1 Sketch The Level Curves Of



Calculus Iii Functions Of Several Variables
The level curves of an elliptic paraboloid are shown as the intersection of a horizontal plane with the graphMar 30, 16 · a plot of the various level curves of a given function function of two variables a function that maps each ordered pair in a subset of to a unique real number graph of a function of two variables a set of ordered triples that satisfies the equation plotted in threedimensional Cartesian space level curve of a function of two variables1 Level Surfaces 2 If one of the Arguments is time we can animate ie w = f(x,y,t) Level Surfaces Given w = f(x,y,z) then a level surface is obtained by considering w = c = f(x,y,z) The interpretation being that on a level surface f has the same value at every pt For example f could represent the temperature at each pt in 3space



How To Sketch Level Curves Youtube



Ti2pdoqmekuwqm
Level curves and level surfaces Because it is a function of x and y, the previous example leads naturally to the topic of level curves (orthogonal projections onto the xyplane of traces in horizontal planes) Given a realvalued function of two real variables, one way to understand the nature of its surface is to make a contour map, a plot inAug 22, 18 · In this section discuss how the gradient vector can be used to find tangent planes to a much more general function than in the previous section We will also define the normal line and discuss how the gradient vector can be used to find the equation of the normal lineEach level curve is the projection of a trace of the surface in a plane of the form z= k Note that at all points (x;y) on a level curve the function have the same value In other words, the function fis constant on a level curve In particular, we used level curves to analyze the function z= xywhose graph is a saddle



Solved Each Diagram Represents The Level Curves Of A Func Chegg Com


Functions Of Several Variables Ximera
A level curve can be drawn for function of two variable ,for function of three variable we have level surface A level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of fA level curve can be described as the intersection of the horizontal plane with the surface defined by f Level curves are also known as contour lines A vertical cross section (parallel to a coordinate plane) of a surface is a twodimensional curve with either the equation or the equation, where c and d are constants$\begingroup$ The map $\b C\to\b R^2$ that takes real/imaginary parts to first/second components will preserve the geometry of figures in the complex plane Like curves, intersections and orthogonality $\endgroup$ – anon May 16 '12 at 21



Level Set Wikipedia


If X X 1 X 2 Represents
Give a vector in the xyplane that is orthogonal to the level curves of the crests and troughs of the wave (which also gives the direction of wave propagation) T 41 Approximate mountains Suppose the elevation of Earth's surface over a 16mi by 16mi region is approximated by theFigure 16 shows both sets of level curves on a single graph We are interested in those points where two level curves are tangent—but there are many such points, in fact an infinite number, as we've only shown a few of the level curvesMy Partial Derivatives course https//wwwkristakingmathcom/partialderivativescourseIn this video we're talking about how to sketch the level curves of



Level Curves Curves Level Stvincent Glogster Edu Interactive Multimedia Posters



Level Sets Math Insight
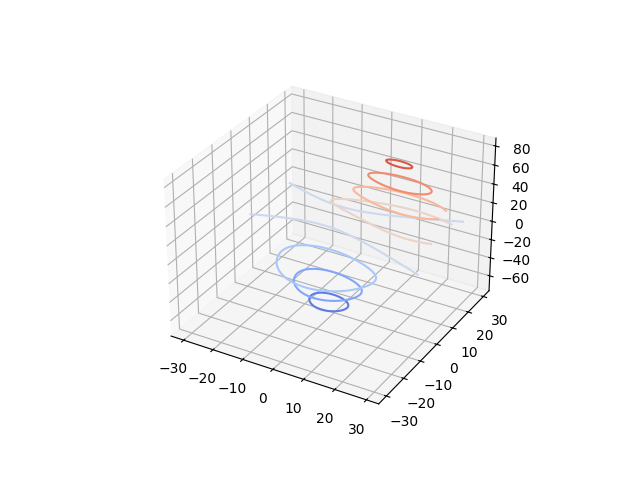


Demonstrates Plotting Contour Level Curves In 3d Matplotlib 3 4 2 Documentation



Calculus Iii Functions Of Several Variables



Level Curves



Level Surfaces



Level Surfaces


X Treme Nerd Interlude Computing And Visualizing Level Curves Of The Days To Derailment Function For The Upcoming Yellow Brick Half Plane New World Order Beeminder Blog



1 Level Curves In The Plane H A Of The Function G A H Y 0 Download Scientific Diagram



Solved Sketch The Level Curves Of F X Y Xy At Levels Chegg Com


Introduction To Functions Of Several Variables Ppt Download



Graph Level Curves For The Plane Z 2x 3y 9 For Two Choices Of Z K Show That The Level Curves For Different Choices Of K Form Distinct



Level Sets Math Insight



11 Copyright C Cengage Learning All Rights Reserved 14 Partial Derivatives Ppt Download



Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube


Business Calculus



Gradients And Level Curves



Make A Contour Plot Showing At Least 3 Level Curves For The Function H X Y Ln X 2 Frac Y 2 4 Study Com



Visualizing Surface And Level Curves Youtube



Level Curves In The Plane E 0 Log A 0 When The Error E M On The Download Scientific Diagram



Level Curves


Level Curves Geogebra Dynamic Worksheet



Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id


Functions Of Several Variables Ximera



Solved Sketch The Level Curves Of The Function F X Y Chegg Com



Level Sets Math Insight


14 1 Functions Of Several Variables



Level Curves In The Plane E 0 Log A 0 When The Error E M On The Download Scientific Diagram



Document


Level Curves And Contour Plots Mathonline



14 Partial Derivatives Copyright Cengage Learning All Rights



1 Level Curves In The Plane H A Of The Function G A H Y 0 Download Scientific Diagram


Business Calculus


Solved 1 Point Each Diagram Represents The Level Curves O Chegg Com
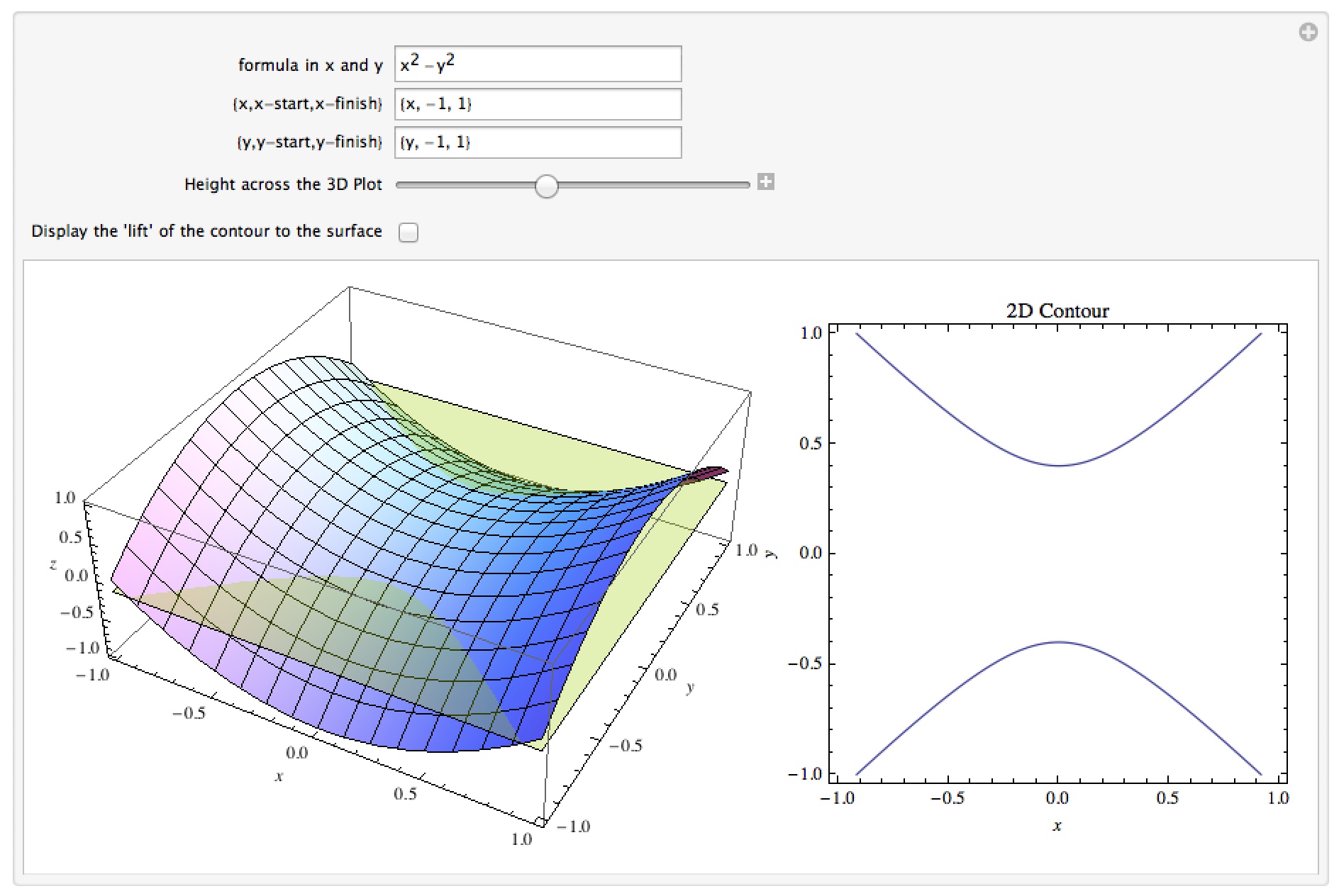


Dr Moretti S Mathematica Notebooks Calculus 3


Level Sets Ximera


Business Calculus



How Can I Project Level Curves Onto The Axis Planes In 3d Usage Julialang



How Does One Project The Gradient At A Point On A Surface Into A Plane Mathematics Stack Exchange



Mitres 18 001 Guide13 Matematica



Solved 2 Graph Level Curves For The Plane2 3y 9 For Two Chegg Com


Functions Of Several Variables Ximera



Cal123 Level Curves And Contour Diagrams Contour Line Curve
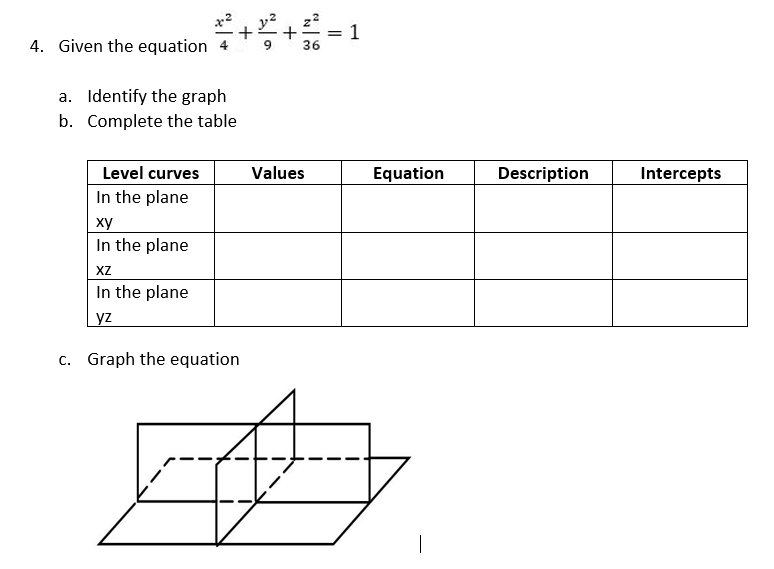


Solved 4 Given The Equation 9 36 Identify The Graph Comp Chegg Com



Level Curves Curves Level Stvincent Glogster Edu Interactive Multimedia Posters



Level Curves Of Functions Of Two Variables Youtube



Level Curves


Level Curves Of V F Ps And Trajectories In The Phase Plane Download Scientific Diagram



Chapter Partial Derivatives
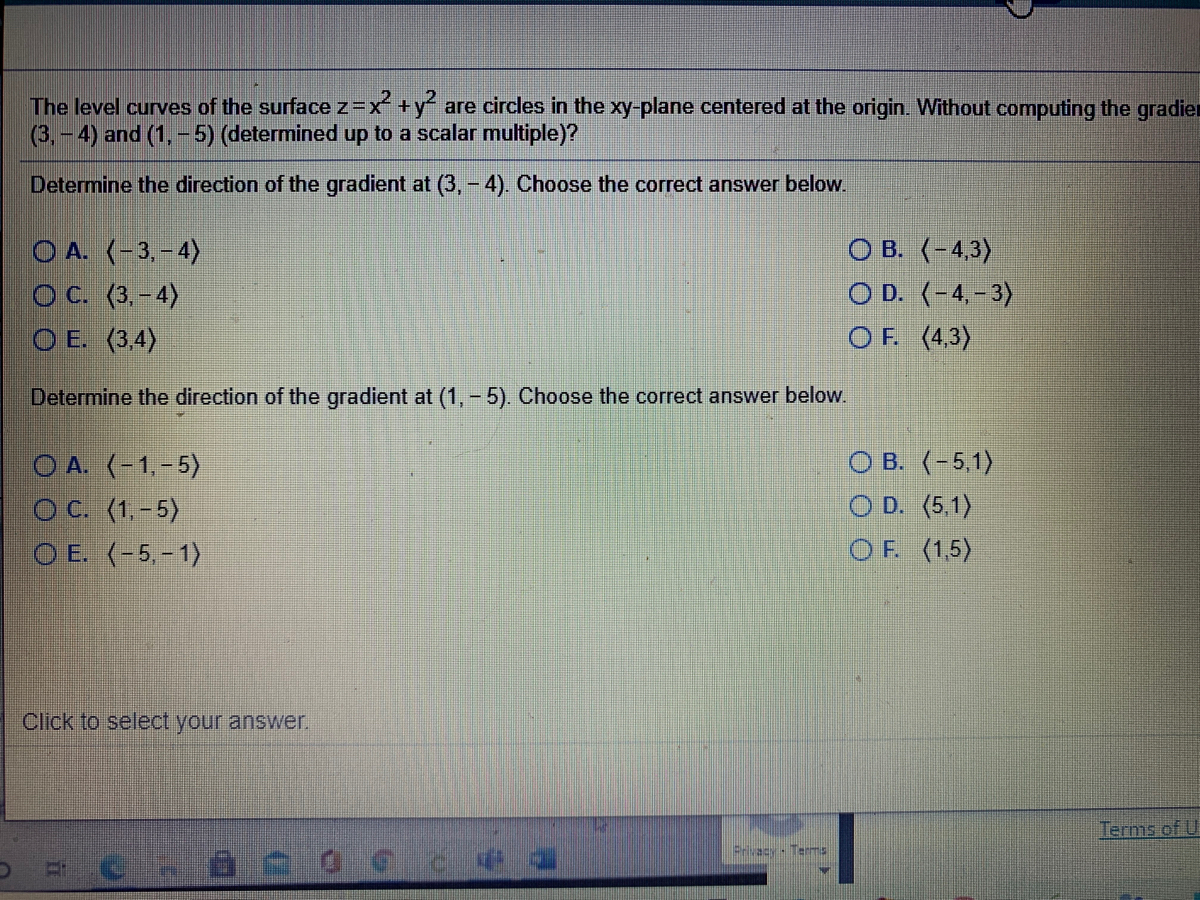


Answered The Level Curves Of The Surface Z X Y Bartleby



Level Set Wikipedia
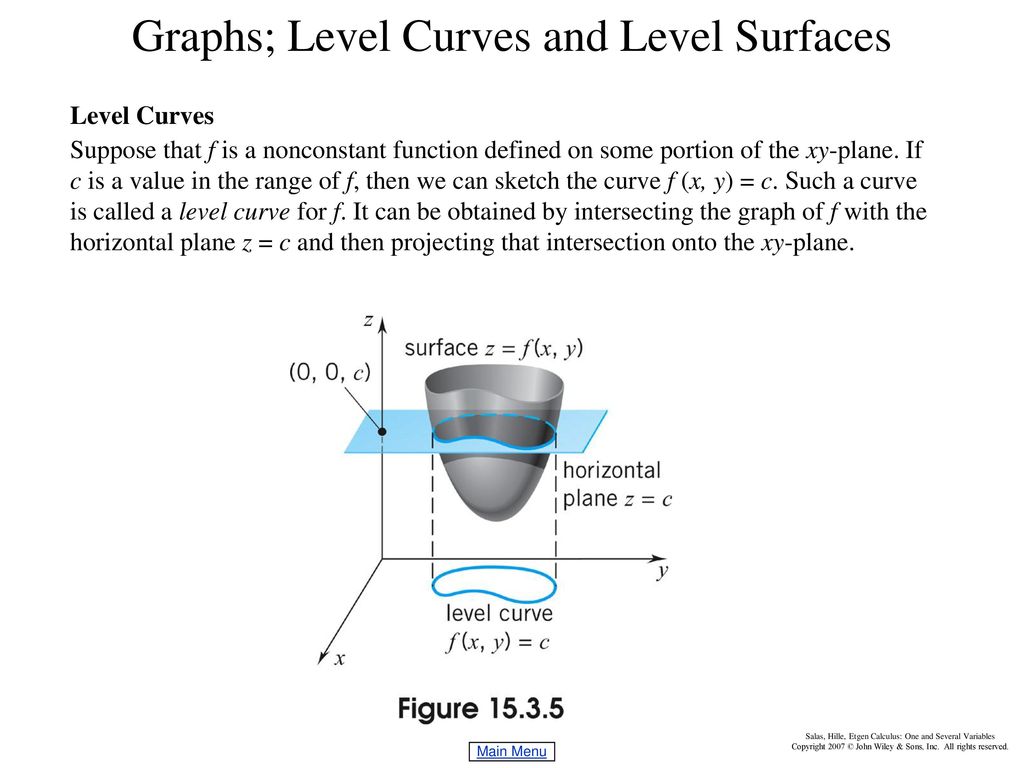


Chapter 15 Functions Of Several Variables Ppt Download
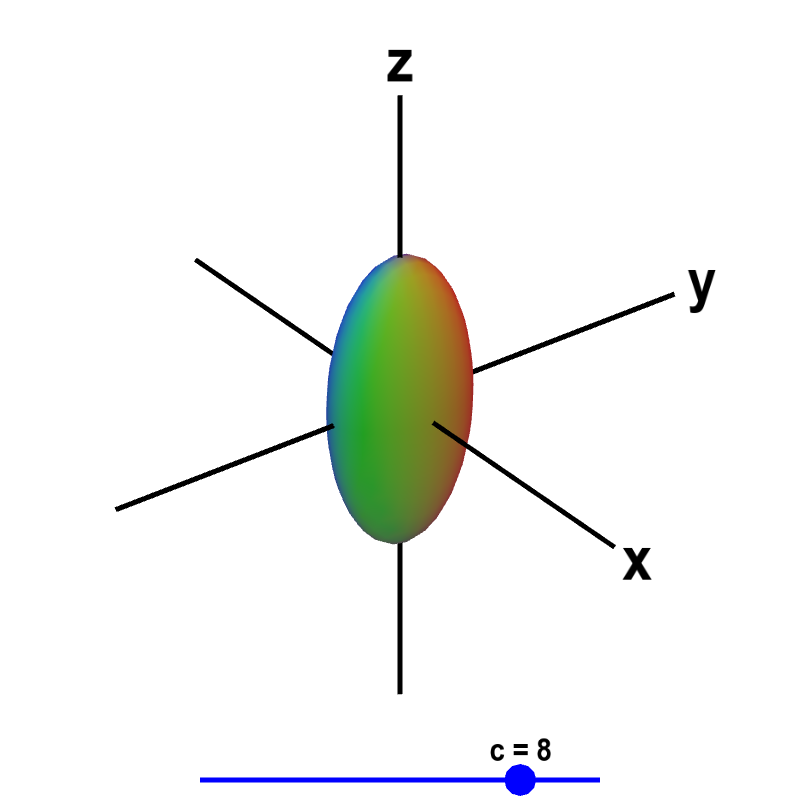


Level Sets Math Insight


Level Curves And Contour Plots Mathonline



Level Curves In Mathbb R 3 Mathematics Stack Exchange
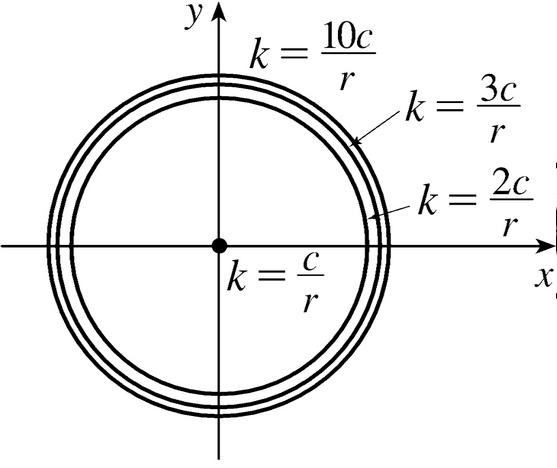


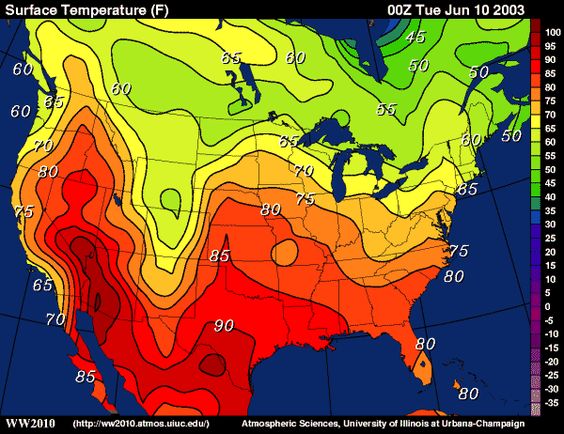
If V X Y Is The Electric Potential At A Point X Y In The Xy Plane Then The Level Curves Of V Are Called Equipotential Curves Because At All Points On Such A


Level Curves From 3d Surfaces Different Layout Geogebra



Mathematics 3 Partial Differentiation Uia Logo Main Menu Calculator Partial Differentiation Introduction Application Contour Curves Application Aircraft Noise Application Temperature Application Electric Resistance Ordinary Differentiation Def



Level Curves Mit 18 02sc Multivariable Calculus Fall 10 Youtube



Answered Parametrized Surfaces Just As You Bartleby
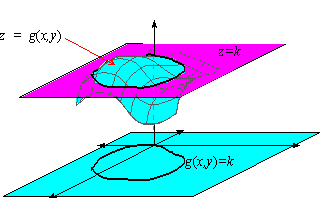


Gradients And Level Curves



0 件のコメント:
コメントを投稿