You need to write sin 2x and cos 2x in terms of tanx such that `sin 2x = (2 tan x)/(1 tan^2 x); tan 2x = ((2sin x)/(1 2sin^2 x))sqrt(1 sin ^2 x) sin 2x = (sin 2x)/(cos 2x) Applying the 3 trig identities sin 2x = 2sin xcos x , and cos 2x = (1 2sin^2 x) cos x = sqrt(1 sin^2 x) We get tan 2x = (2sin xcos x)/(1 2sin^2 x) = = ((2sin x)/(1 2sin^2 x))sqrt(1 sin^2 x)Calculus Examples Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by sin(x) cos(x) sin ( x) cos ( x) Write sin(x) sin ( x) as a fraction with denominator 1 1 Cancel the common factor of sin(x) sin ( x) Tap for more steps Cancel the common factor Rewrite the expression

How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
Tan 2x formula in terms of sin x
Tan 2x formula in terms of sin x- You can check some important questions on trigonometry and trigonometry all formula from below 1 Find cos X and tan X if sin X = 2/3 2 In a given triangle LMN, with a right angle at M, LN MN = 30 cm and LM = 8 cm Calculate the values of sin L, cos L, and tan L 3\(\cos 2X = \cos ^{2}X – \sin ^{2}X \) Hence, the first cos 2X formula follows, as \(\cos 2X = \cos ^{2}X – \sin ^{2}X\) And for this reason, we know this formula as double the angle formula, because we are doubling the angle Other Formulae of cos 2X \(\cos 2X = 1 – 2 \sin ^{2}X \) To derive this, we need to start from the earlier derivation




Integrate Tan 2x By Parts
2 tan x = 2 (sin x)/ (cos x) (1) Since t = tan(x / 2) = sin (x / 2) cos (x / 2) and sin2(x / 2) cos2(x / 2) = 1, solve for sin(x / 2) = t √1 t2 and cos(x / 2) = 1 √1 t2 (here I am assuming that x / 2 ∈ 0, π / 2) the other cases are similar) Now you can use the formulas that give you the sin and cos of double angles, and you are doneThe cosine of double angle is equal to the quotient of the subtraction of square of tangent from one by the sum of one and square of tan function cos 2 θ = 1 − tan 2 θ 1 tan 2 θ It is called the cosine of double angle identity in terms of tangent function
Tan2x Formulas Tan2x Formula = 2 tan x 1 − t a n 2 x We know that tan (x) = sin (x)/cos (x)They are Arc cos x, Arc tan x, Arc cot x, Arc sec x, and Arc csc xSolve for x sin(2x)=tan(x) Rewrite in terms of sines and cosines Rewrite the equation as Solve for The period of the function is so values will repeat every radians in both directions, for any integer, for any integer Set up the equation to solve for Solve the equation for
The equation x = sin y defines y as a multiplevalued function of x This function is the inverse of the sine and is symbolized Arc sin x The inverse functions of the cosine, tangent, cotangent, secant, and cosecant are defined in a similar way;After doing so, the first of these formulae becomes sin (x x) = sin x cos x cos x sin x so that sin2x = 2 sin x cos x And this is how our first doubleangle formula, so called because we are doubling the angle (as in 2A) Practice Example for Sin 2xFormula sin 2 θ = 2 tan θ 1 tan 2 θ A trigonometric identity that expresses the expansion of sine of double angle function in terms of tan function is called the sine of double angle identity in tangent function




Rewrite The Expression In Terms Of The First Power Of The Cosine Cos 4xtan 2x Brainly Com



3
Simplify\\frac {\sec (x)\sin^2 (x)} {1\sec (x)} simplify\\sin^2 (x)\cos^2 (x)\sin^2 (x) simplify\\tan^4 (x)2\tan^2 (x)1 simplify\\tan^2 (x)\cos^2 (x)\cot^2 (x)\sin^2 (x) trigonometricsimplificationcalculator enThe figure at the right shows a sector of a circle with radius 1 The sector is θ/(2 π) of the whole circle, so its area is θ/2We assume here that θ < π /2 = = = = The area of triangle OAD is AB/2, or sin(θ)/2The area of triangle OCD is CD/2, or tan(θ)/2 Since triangle OAD lies completely inside the sector, which in turn lies completely inside triangle OCD, we have Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomes \(tan(aa) =\frac{ tan a tan a }{1 tan a tana}\) \(Tan 2a =\frac{2tan a}{1tan^{2}a} \) Practice Example for tan 2 theta Question




Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic
The formula there gives texsin(x)=\pm\frac{tanx}{1tan^2x}/tex so by being as brief as possible, this is the best that could be done They don't mention for what domain it is plus and where is it minusWe can easily derive this formula using the addition formula for Sin angles We know that the addition formula for sin is given as Where X and Y are the two angles In the above formula replace Y by X, with the assumption that both angles X and Y are equal Thus, Hence Sin 2x = 2 Sin x Cos x4 Chapter 10 Techniques of Integration EXAMPLE 1012 Evaluate Z sin6 xdx Use sin2 x = (1 − cos(2x))/2 to rewrite the function Z sin6 xdx = Z (sin2 x)3 dx = Z (1− cos2x)3 8 dx = 1 8 Z 1−3cos2x3cos2 2x− cos3 2xdx Now we have four integrals to evaluate Z 1dx = x and Z




Misc 10 Sin X 1 4 Find Sin X 2 Cos X 2 Tan X 2 Chapter 3



Prove Sin2x 2tanx 1 Tan 2x Socratic
In this video, I derive the following identitiessin(x) = 2*t / (1 t^2)cos(x) = (1 t^2) / (1 t^2)These identities are important when it comes to simpli Change to sines and cosines then simplify 1 tan2x = 1 sin2x cos2x = cos2x sin2x cos2xFormula to Calculate tan2x Tan2x Formula is also known as the double angle function of tangent Let's look into the double angle function of tangent ie, tan2x Formula is as shown below tan 2x = 2tan x / 1−tan2x where, tan x = Opposite Side / Adjacent Side tan 2x = Double angle function of tan x tan 2 x = Square funtion of tan x



What Is The Difference Between Tanx Raise To 2 And Tan Square X Quora




What Is Integral Of Sin2x Tan2x Quora
Transcript These formulas can be derived using x y formulas For sin 2x sin 2x = sin (x x) Using sin (x y) = sin x cos y cos x sin y = sin x cos x sin x cos For this first we calculate sec a and cos a We know that sec2 a = 1 tan2 a sec a = √ (1𝑡𝑎𝑛2 a) We convert tan−1 to sin−1 sec a = √ (1𝑥2) 1/cos𝑎 = √ (1𝑥2) 1/√ (1 𝑥^2 ) = cos𝑎 𝒄𝒐𝒔𝒂 = 𝟏/√ (𝟏 𝒙^𝟐 ) We know that sin a = √ ("1 – cos2 a" ) sin a = √ ("1 –" (1/√ (1 𝑥^2 ))^2 ) sin a = √ ("1 –" 1/ (1 𝑥2)) sin a = √ ( (1 𝑥2 − 1)/ (1 𝑥2)) = √ ( (𝑥2 )/ (1 𝑥2)) = √ (𝑥^2Formulas from Trigonometry sin 2Acos A= 1 sin(A B) = sinAcosB cosAsinB cos(A B) = cosAcosB tansinAsinB tan(A B) = A tanB 1 tanAtanB sin2A= 2sinAcosA cos2A= cos2 A sin2 A tan2A= 2tanA 1 2tan A sin A 2 = q 1 cosA 2 cos A 2
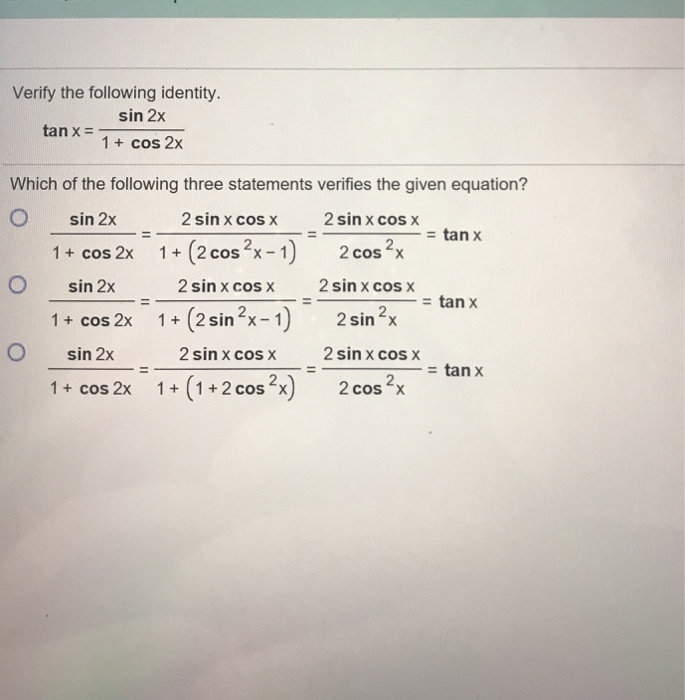



Verify The Following Identity Tan X Sin2x 1 Cos Chegg Com
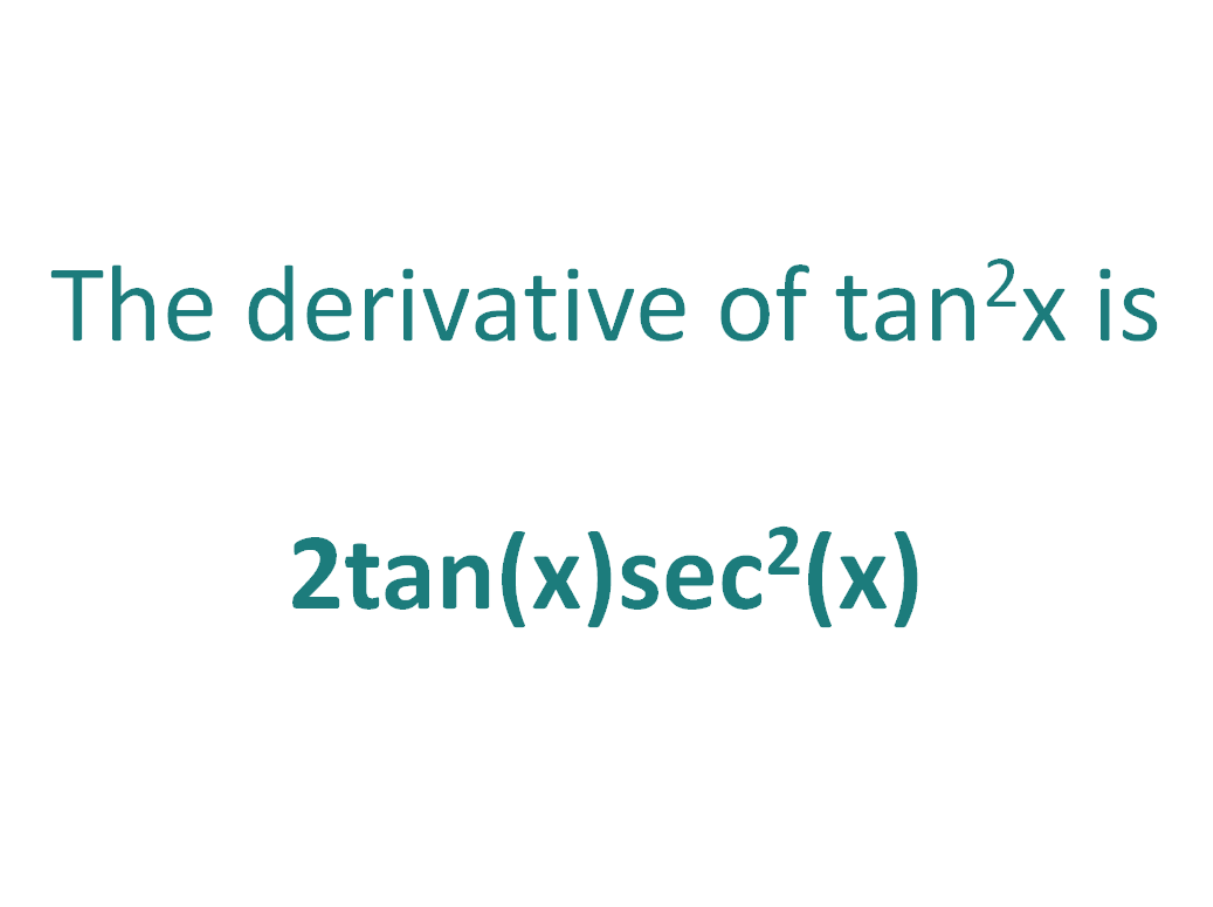



The Derivative Of Tan 2x Derivativeit
Alternatively, we could get the expression for cos(2x) in terms of sin(x) cos(2x) = (1 sin²(x)) sin²(x) = 1 2sin²(x) So, there are three formulas forTo rewrite the sine function in terms of tangent, follow these steps Start with the ratio identity involving sine, cosine, and tangent, and multiply each side by cosine to get the sine alone on the left Replace cosine with its reciprocal function Solve the Pythagorean identity tan 22 tan x = 2 (sin x)/ (cos x) (1) = 2 (sin x) (cos x)/ (cos²x)
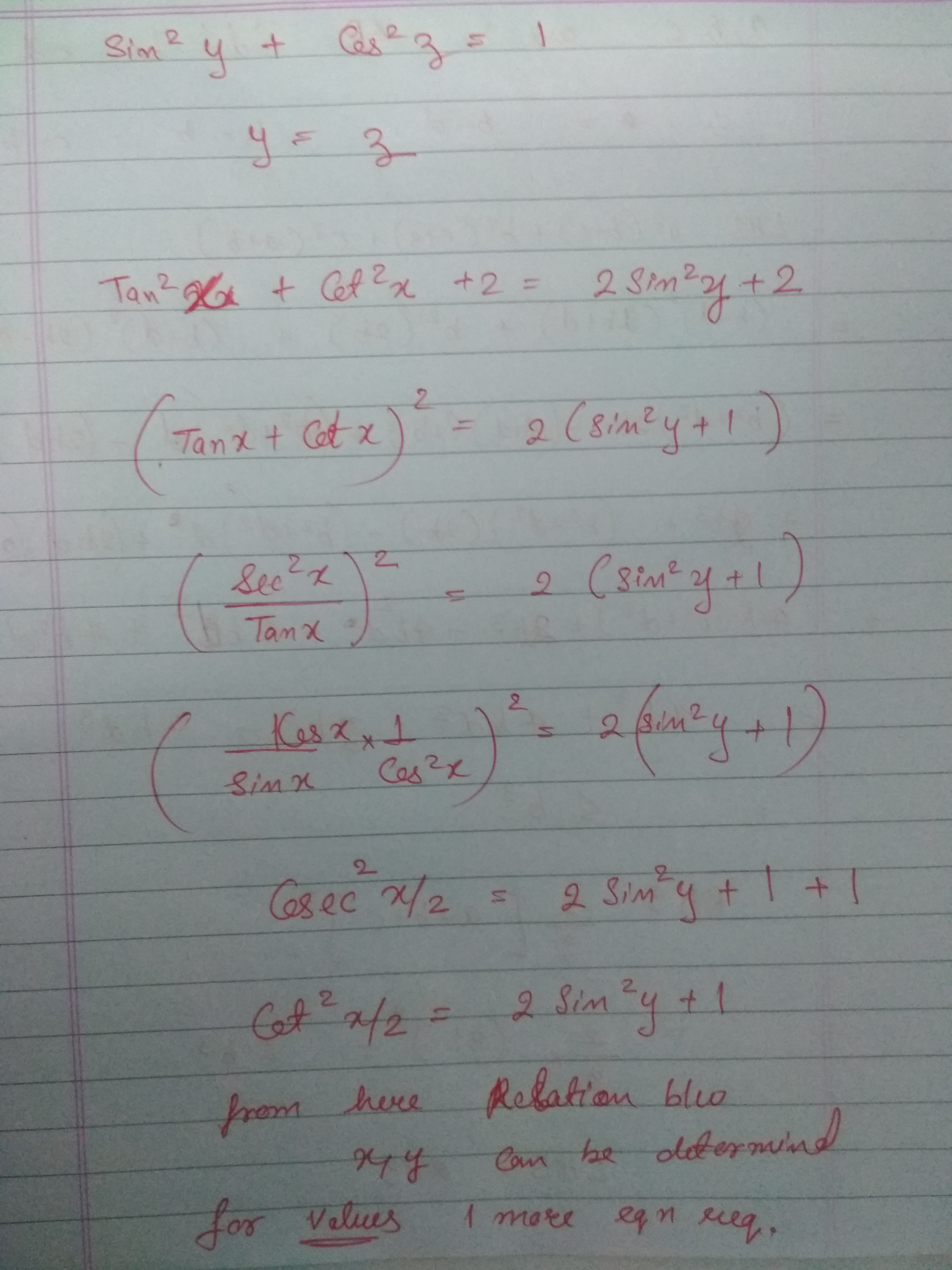



Solve For X Y And Z If Tan 2x Cot 2x 2sin 2y And Sin 2y Cos 2z 1 Askiitians




How Do You Find A Double Angle Formula For Sec 2x In Terms Of Only Csc X And Sec X Socratic
The functions sine, cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functions Their usual abbreviations are (), (), and (), respectively, where denotes the angle The parentheses around the argument of the functions are often omitted, eg, and , if an interpretation is unambiguously possible The sine of an angle is definedX Therefore, tan 2 x = ( sin 2 x / 1 − 2 sin 2 x) Is it possible to do it in terms of cosWhat is the 2tanx formula?



What Is The Formula Of Tan2x Quora




Cos X Plus Sin X Upon Cos X Minus Sin X Minus Cos X Minus Sin X Upon Cos X Plus Sin X Is Equal To 2 Brainly In
From what I know about the graph of the tangent, I know that the tangent will equal 1 at 45° after every 180° These solutions for tan( x /2) are at 0° 45°, 180° 45°, 360° 45° , and so forthAngle formulas for both cosine and sine tan x/2 = (sin x/2)/ (cos x/2) (quotient identity) tan x/2 = ±√ (1 cos x)/ 2 / ±√ (1 cos x)/ 2 (halfangle identity) tan x/2 = ±√ (1 cos x)/ (1 cos x) (algebra) Halfangle identity for tangent • There are easier equations to the halfangle identity for tangent equation The tangent formula is easy to get just divide But it turns out to be easier if you don't divide the final forms, but rather the "raw" collected terms from above sin 3A = 3 cos² A sin A − sin³ A cos 3A = cos³ A − 3 cos A sin² A tan 3A = sin 3A / cos 3A tan 3A = (3 cos² A sin A − sin³ A) / (cos³ A − 3 cos A sin² A)




Trigonometric Functions With Their Formulas



T Tan X 2 Weierstrass Substitution Youtube
Cos 2x = (1tan^2 x)/(1 tan^2 x)` Plugging `tan x = sqrt6/3` in the formulas above yieldsTrigonometric function of sin 2A in terms of tan A is also known as one of the double angle formula We know if A is a number or angle then we have, sin 2A = 2 sin A cos A ⇒ sin 2A = 2 s i n A c o s A ∙ cos 2 A ⇒ sin 2A = 2 tan A ∙ 1 s e c 2 A ⇒ sin 2A = 2 t a n A 1 t a n 2 A There for sin 2A = 2 t a n A 1 t a n 2 A Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin and




Powers Of Trigonometric Functions




Trigonometric Identity Challenge Sin 2 Cos 2x Tan 2x Youtube
We will develop formulas for the sine, cosine and tangent of a half angle Half Angle Formula Sine We start with the formula for the cosine of a double angle that we met in the last section cos 2θ = 1− 2sin 2 θHalfangle formula for , however, we have Notice that we mentally made the substitution when integrating Another to express the remaining factors in terms of sine Then substitute (b) If the power of sine is odd , save one sine factor and use sec2x 1 tan2x tan x n 2k, k 2 sec2x y tanmx secnx dx x tanmx secnx dx 1 11 sec 11 2 9 sec 9Derivatives of the Trigonometric Functions Formulas of the derivatives of trigonometric functions sin (x), cos (x), tan (x), cot (x), sec (x) and csc (x), in calculus, are presented along with several examples involving products, sums and quotients of trigonometric functions




The Value Of Lim X Pi 2 Tan 2x Sqrt 2sin 2x 3sinx 4 Sqrt Sin 2 X 6sinx 2 Is Equal To




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube
Trigonometric Identities Solver \square!Formulas and identities of sin 2x, cos 2x, tan 2x, cot 2x, sec 2x and cosec 2x are known as double angle formulas because they have angle double of the angle present in their formulas Sin 2x Formula Sin 2x formula is 2sinxcosx Image will be uploaded soon Sin 2x =2 sinx cosx Derivation of Sin2x Formula Before going into the actual proof Sin2x= Tan2x*Cos2x but note that Cos^2(2x)=1/Sec^2(2x) using sec^2(2x)=1 tan^2(2x) we then get Sin2x=Tan2x/Sqrt(1tan^2(2x)) this is all ok but sin2x=2sinxcosx so you need to do the same for cos2x and find cosx in terms of tan2x thus replace it into the expression above




Math34 Trigonometric Formulas



3
The Pythagorean formula for tangents and secants There's also one for cotangents and cosecants, but as cotangents and cosecants are rarely needed, it's unnecessary Identities expressing trig functions in terms of their supplements Sum, difference, and double angle formulas for tangent The half angle formulas The ones for sine andGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!243 The Substitution z = tan (x/2) Suppose our integrand is a rational function of sin (x) and cos (x) After the substitution z = tan (x / 2) we obtain an integrand that is a rational function of z, which can then be evaluated by partial fractions
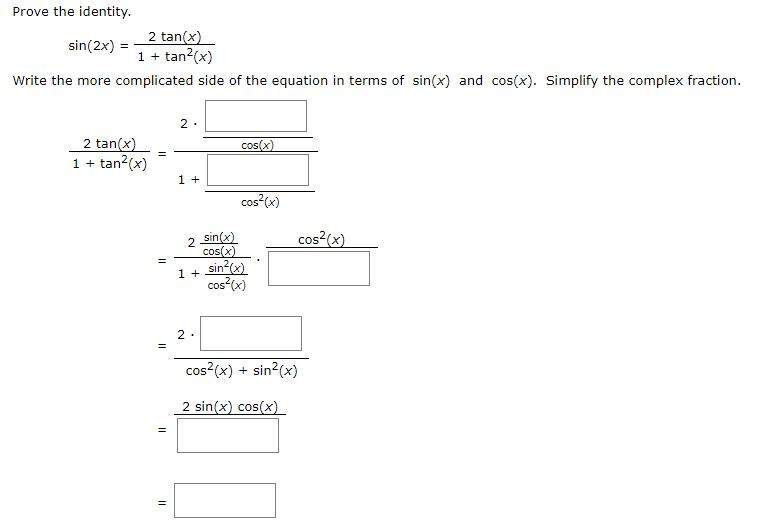



Prove The Identity 2 Tan X Sin 2x 1 Tan2x Write Chegg Com




Sec 1 1 Tan 2x 1 Tan 2 X
Derivative Of sin^2x, sin^2(2x) – The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variable Common trigonometric functions include sin(x), cos(x) and tan(x) For example, the derivative of f(x) = sin(x) is represented as f ′(a) = cos(a) f ′(a) is the rate of change




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




Verify The Identity 2 Tan X Sin 2x 1 Tan2 X 2 Chegg Com




Section 7 3 Double Angle Half Angle And Sum



Http Www Mayfieldschools Org Downloads 4 8 double angle formulas key Pdf




Tan 2x Formula What Is Tan 2x Formula Examples




Double Angle Formulas What Are Double Angle Formulas Examples




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Problem 4 Using The Sin And Cos Addition Formulas Chegg Com




Weierstrass Substitution Wikipedia




Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Download




Integrate Tan 2x By Parts




Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2
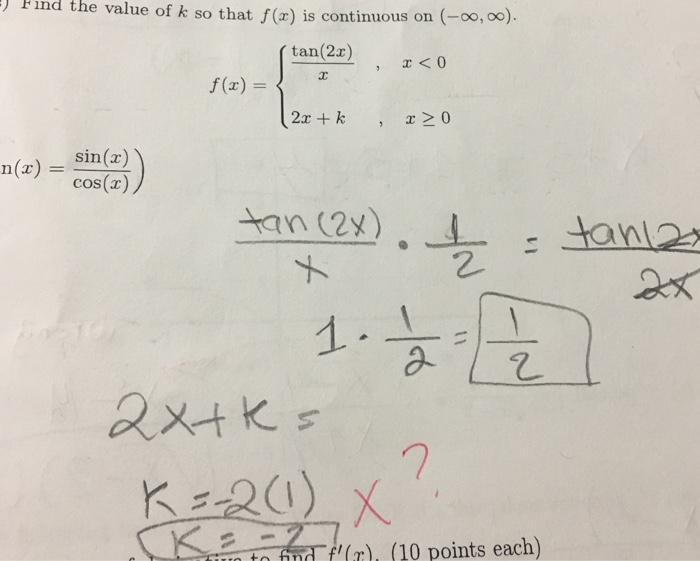



Find The Value Of K So That F N Is Continuous On Chegg Com



Tan2x ただの悪魔の画像




Cos2x 1 Sin2x Tan Pi 4 X Double And Half Angle Identity Youtube




If Cos X Y 4 5 Sin X Y 5 13 And X And Y Lies Between 0 And P 4 Then What Is The Value Of Tan2x Quora



Q Tbn And9gcsxz Hkczzvj4wy3gx0dbnqphk3hi Cp Rmi Vgbp2veivzqwuc Usqp Cau
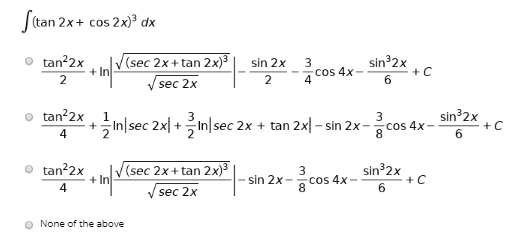



Answered Stan 2x Cos 2x Dx Tan 2x 2 V Sec 2x Bartleby




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube




If Sin X 5 3 And 0 Lt X Lt P 2 Find The Value Of Sin 2x Cos 2x Tan 2x Brainly In




Compound Angle Identity Tan 3x Formula Derivation Youtube




Dana Harrington I Need Some Math Help From My Mtbos Iteachmath Precalcchat Friends I Am Stumped On How To Explain This We See All 6 Answers When We Graph We




Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube
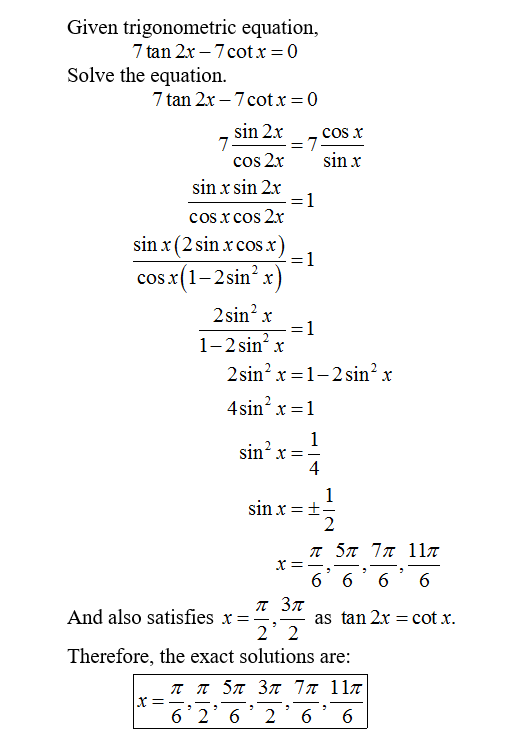



Given Trigonometric Equation 7 Tan 2x 7 Cotx 0 Chegg Com



What Is The General Solution Of X For Tan X Tan2x 1 Quora




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic




Prove The Identity 2 Sin X Cos X Tan 2x 2 Chegg Com




Section 7 3 Double Angle Half Angle And Chegg Com
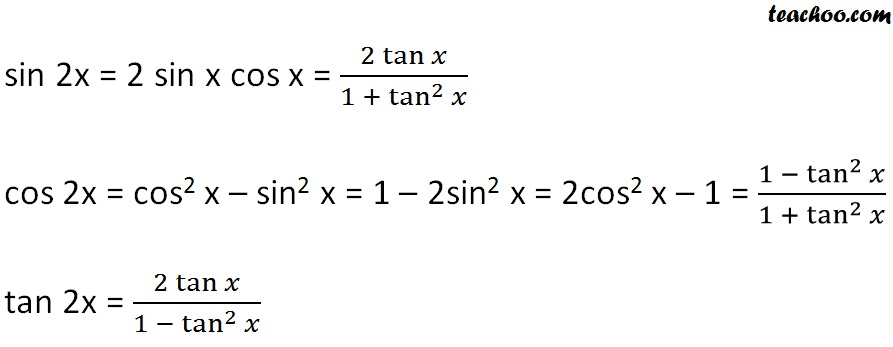



Half Angle Formulas Power Reducing Formulas 2x 3x Formula Provin




Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic
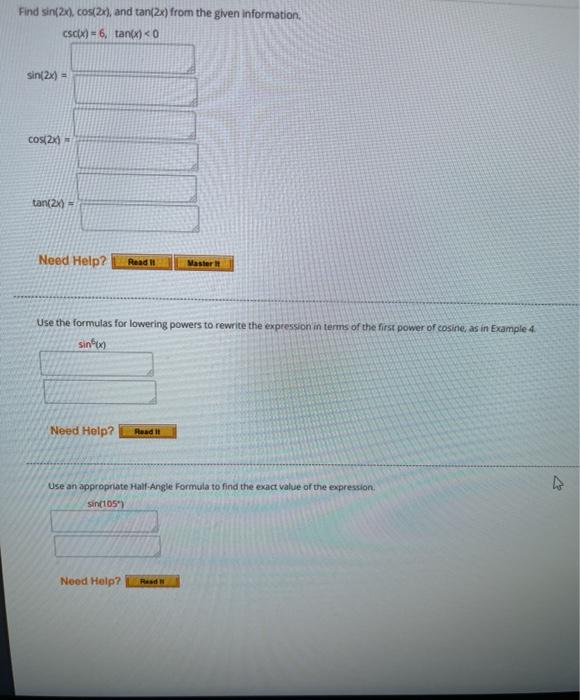



Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Vii Let Y Tan 1 Sin 4x V1 Sin 4x Tan 1 Cos 2x Sin 2x 2 Tan Cos 2x Sin 2x Cos 2x Sin 2x Cos 2x Sin 2x Dividing




Find A Sin 2x B Cos 2x And C Tan 2x If Cos X Chegg Com




Solve The Trigonometric Equation Tan X Tan 2x Tan X Tan 2x 1




Tangent Half Angle Formula Wikipedia




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero
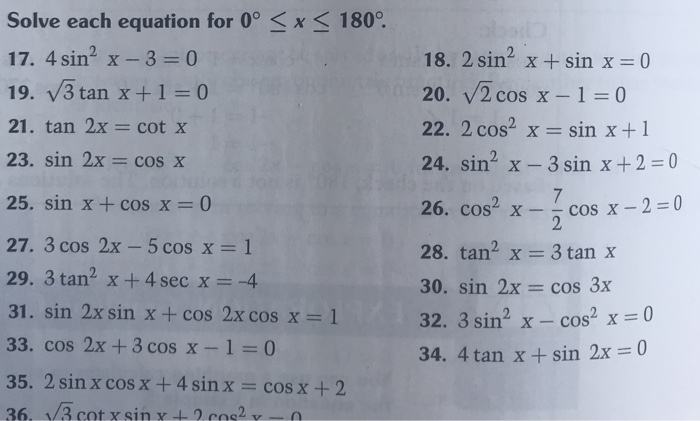



Solve Each Equation For 0 X 180 17 4 Sin2 Chegg Com




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Trig Identity Sec2x Minus Tan2x T10 Youtube



Solved A First Rewrite The Left Hand Side 1 Tan 2x In Terms Of Sin X And Cos X B Next Add The Two Terms In The Expression You Got In Part




Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Cos2xu003dcosx




Tangent Half Angle Formula Wikipedia




Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube




Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com
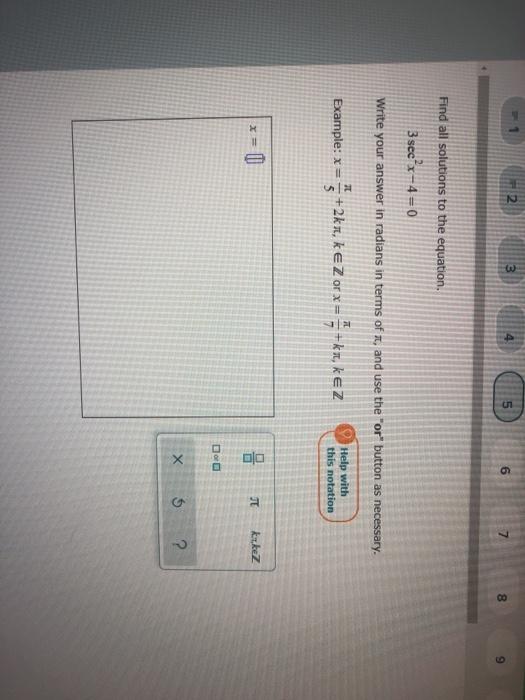



2 3 4 5 6 7 1 Find Sin 2x Cos 2x And Tan 2x If Sinx Chegg Com
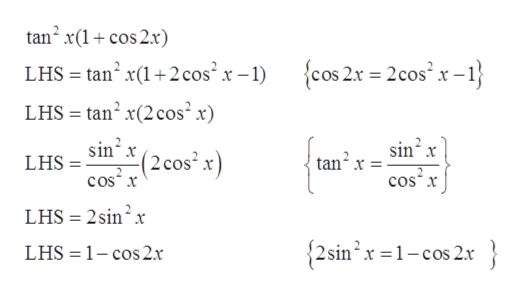



Answered Tan2x 1 Cos2x 1 Cos2x Verify The Bartleby
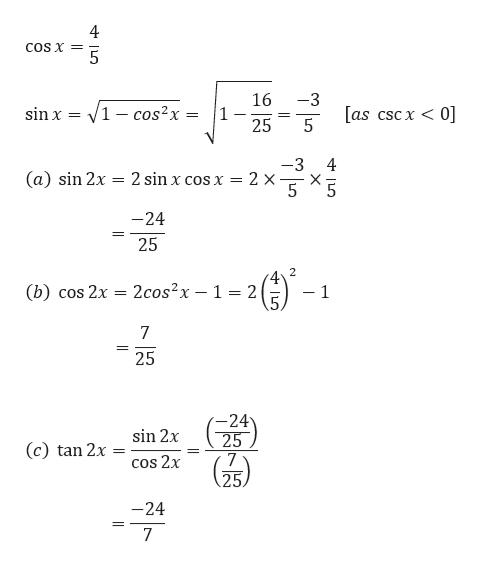



Answered If Cosx 4 5 Cscx 0 Then Sin 2x Bartleby




Se Skills Le Angle Formulas Find Sin 2x Cos 2 X And Chegg Com



If T Tanx How Can One Express Cosx 2 In Terms Of T Quora




Ex 3 3 19 Prove Sin X Sin 3x Cos X Cos 3x Tan 2x



Derivatives Of Trigonometric Functions
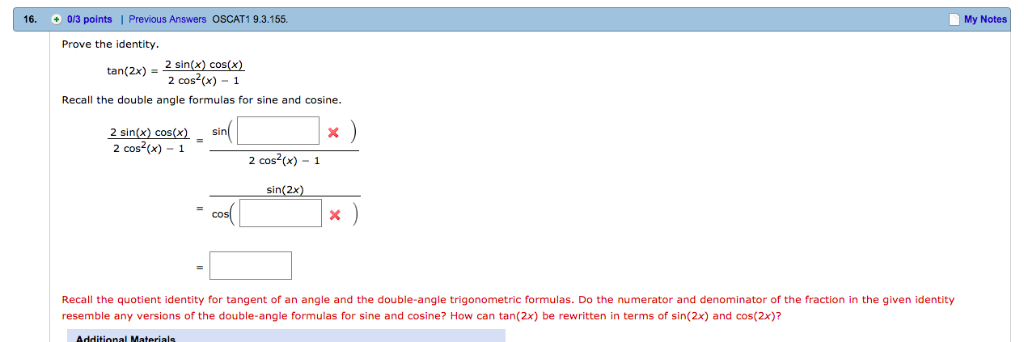



16 0 3 Points Previous Answers Oscat1 9 3 155 My Chegg Com
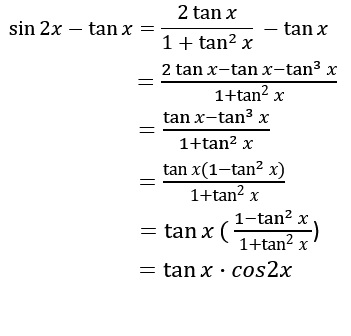



Sin2x Tanx Complete The Identity Socratic




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11
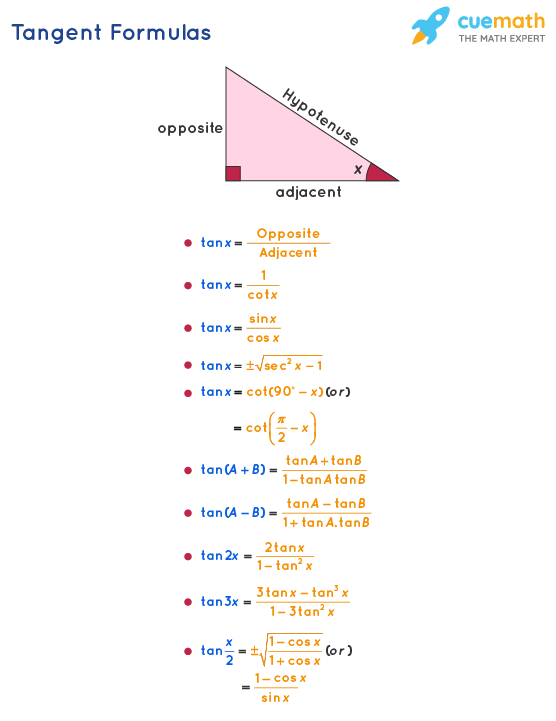



Tangent Formula What Are Tangent Formulas Examples
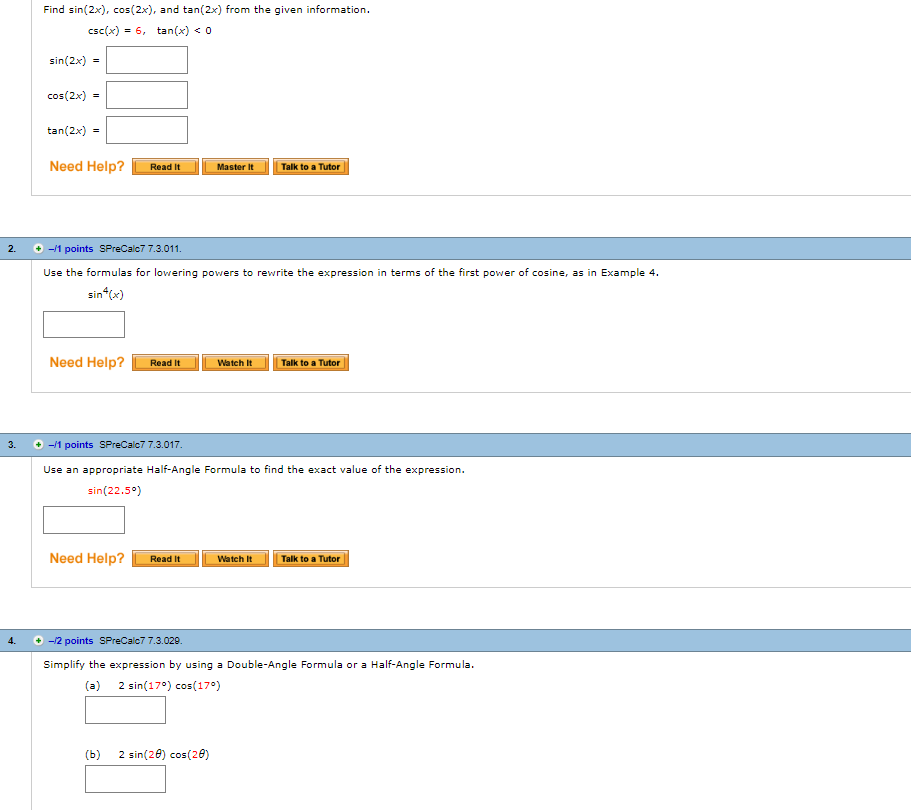



Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




Tan 2x Sin 2x Tan 2x Sin 2x




Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11



If Sin 3x Cos X Then Find Tan 2x Quora
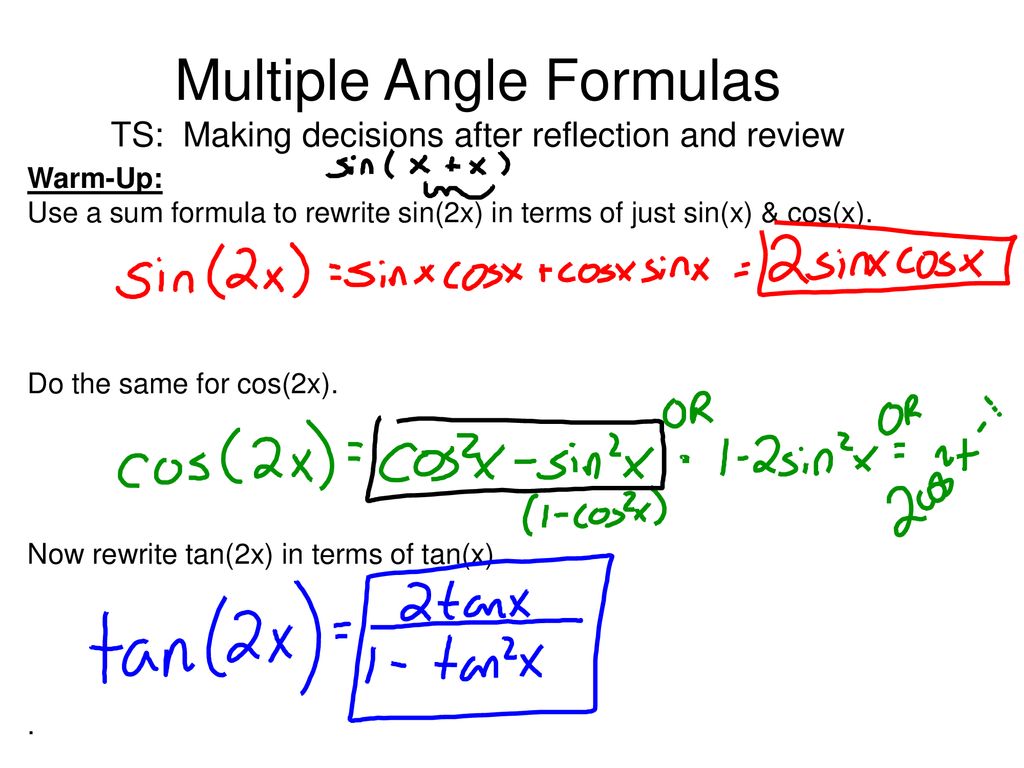



Multiple Angle Formulas Ts Making Decisions After Reflection And Review Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Ppt Download
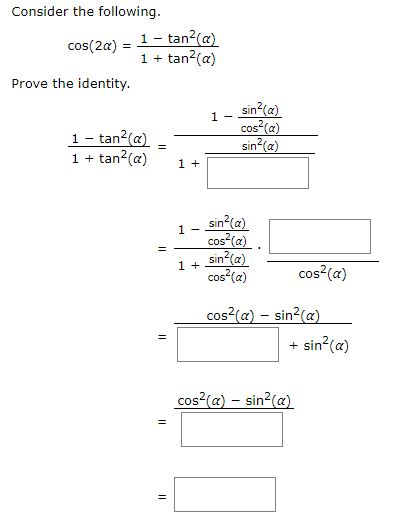



Prove The Identity 2 Tan X Sin 2x 1 Tan2x Write Chegg Com




Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube




Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Powerpoint




Write Cos2x In Terms Of Tanx Double Angle Transformation Youtube




Weierstrass Substitution Wikipedia



What Are The Formulas Of Cos 2x Quora




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube




5 5 Multiple Angle And Product Sum Formulas Find All Solutions In Ppt Download
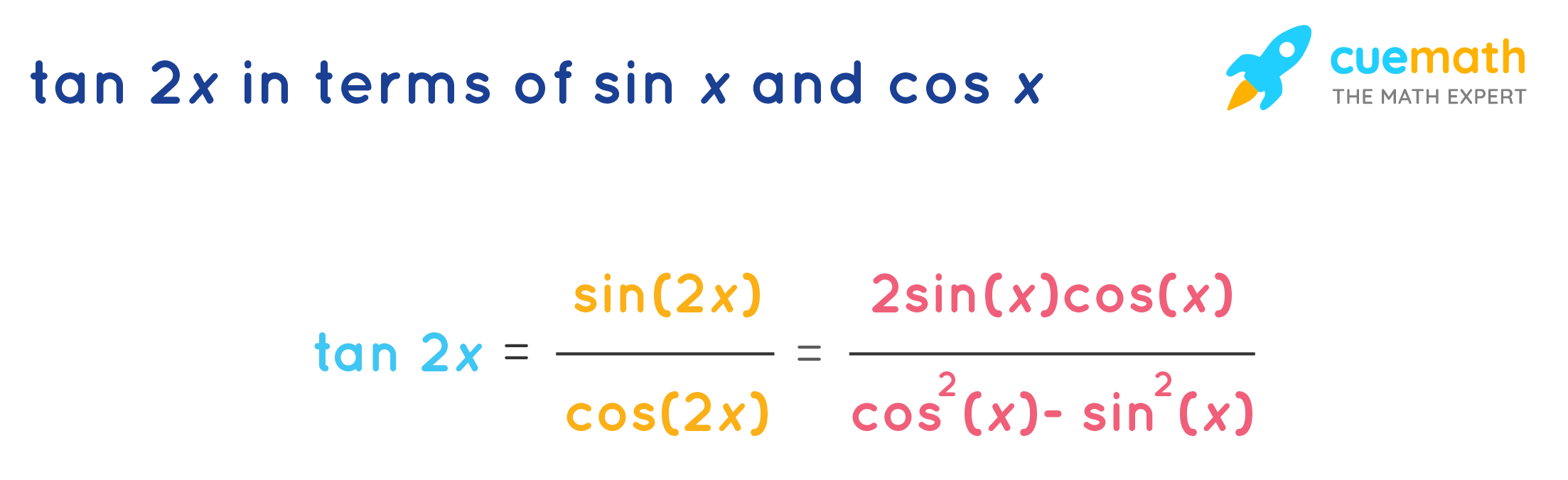



Tan 2x Formula What Is Tan 2x Formula Examples




Tan2x Sin2x Tan2x Sin2x 5 1 Brainly In



Trigonometric Functions Of Double Angles Expressed By The Tangent Function Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities Examples



How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora




Challenge Trigonometric Equation Tan2x 8 Cos 2x Cot X Youtube



3



0 件のコメント:
コメントを投稿